参加了一次机器学习竞赛，用到了LightGBM模型，在此进行一些要点的解析以便答辩。

首先LightGBM是一种GBDT（梯度提升决策树），B代表Boosting，是一种ensemble的策略，G代表使用梯度计算拟合残差的方向。与LightGBM类似的是xgboost，但是LightGBM在性能方面上有不小的提升。

CART 决策树

LightGBM是一种集成模型，先从其最基础的学习器开始介绍。GBDT模型通常都使用CART（Classification And Regression Tree）作为一个基础的学习器。

以下是一个CART决策树的示意图。

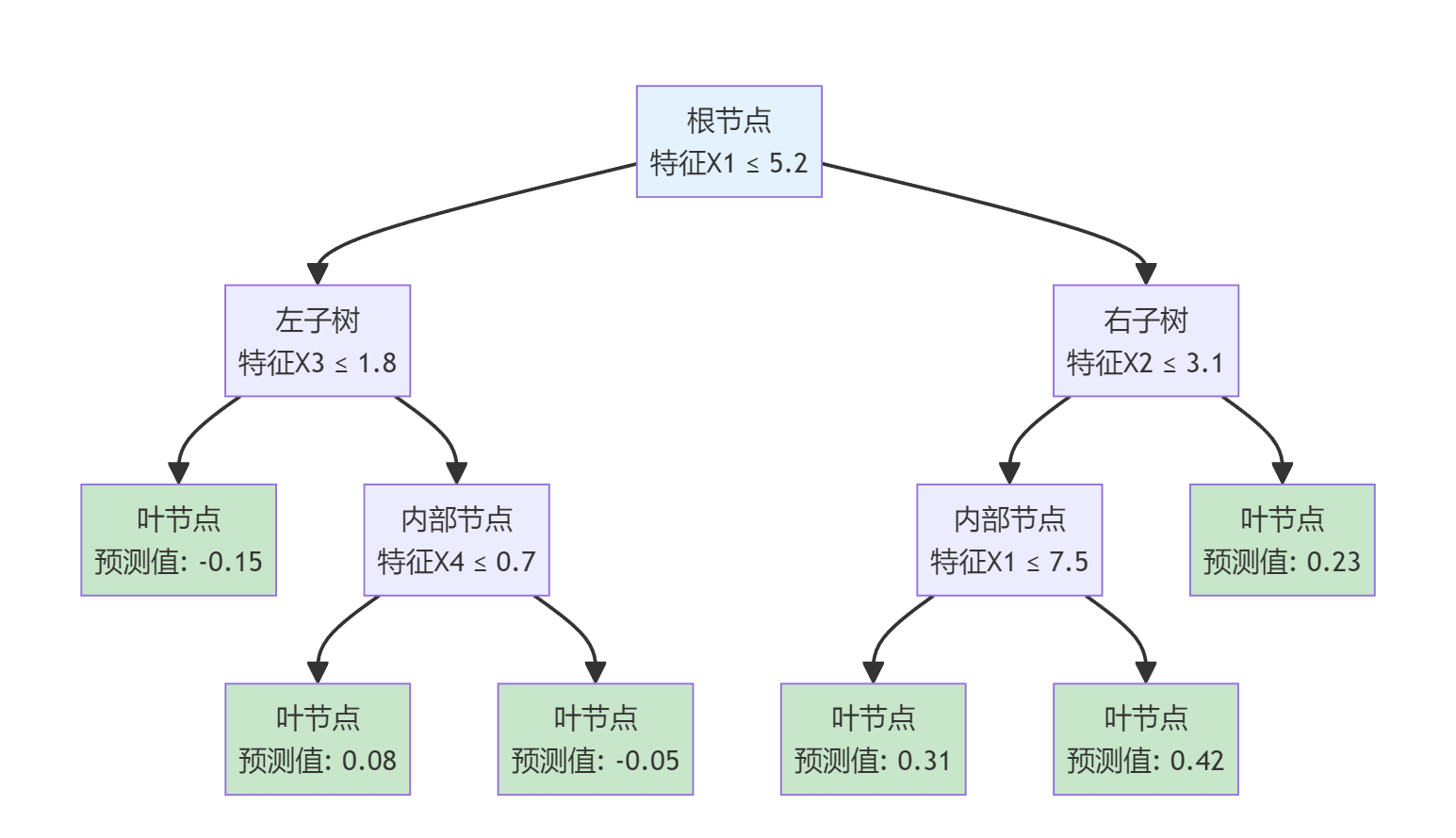
分割策略

CART主要的几个特点是使用基尼系数和其增益（分类情况下）作为提升的评估（其他使用信息熵和信息增益），且每个节点都是严格的二分，不会有多分支。

普通CART分割方式和其他决策树基本相同，先遍历要按哪个特征进行分割，再从这个特征里的值遍历出最佳分割点。

数学表达如下：

先定义 R_L和 R_R，即两个子节点的集合。

接下来是选择出 j^*, s^* 的方式

j^*, s^*的性质如上，即最小化加权的 D，最基础的具体选择方式是通过遍历（也有优化方式）

这里的 D 是数据的不纯度，分类任务使用基尼系数计算，回归任务使用MAE计算。

Boosting

boosting是一种ensemble集成策略，与之同级的有bagging和stacking。

bagging的思想是从原始数据随机采样出多个子数据集，再使用多个基学习器进行预测，最后对所有基学习器的结果进行聚合得到最终结果（例如分类聚合方式使用多数投票，回归聚合方式使用取平均），代表算法有随机森林。

stacking的思想将数据分为k份，对每一份使用一个单独的基学习器（基本可以是任何机器学习模型）进行训练，最后再训练一个元学习器（多用简单模型，如线性回归）组合每个基学习器，找到最优的组合方式得到最终结果。

boosting的思想是先用一个学习器学习到基础的数据，再使用后续的学习器学习上一个学习器和真实值之间的残差。如此往复，最后将所有学习器输出的值加权求和，得到最终结果。

流程如下所示，红色方块的残差即模型的输出，对于第一个分类器来说，他输出的残差就是一个基础的预测数据：

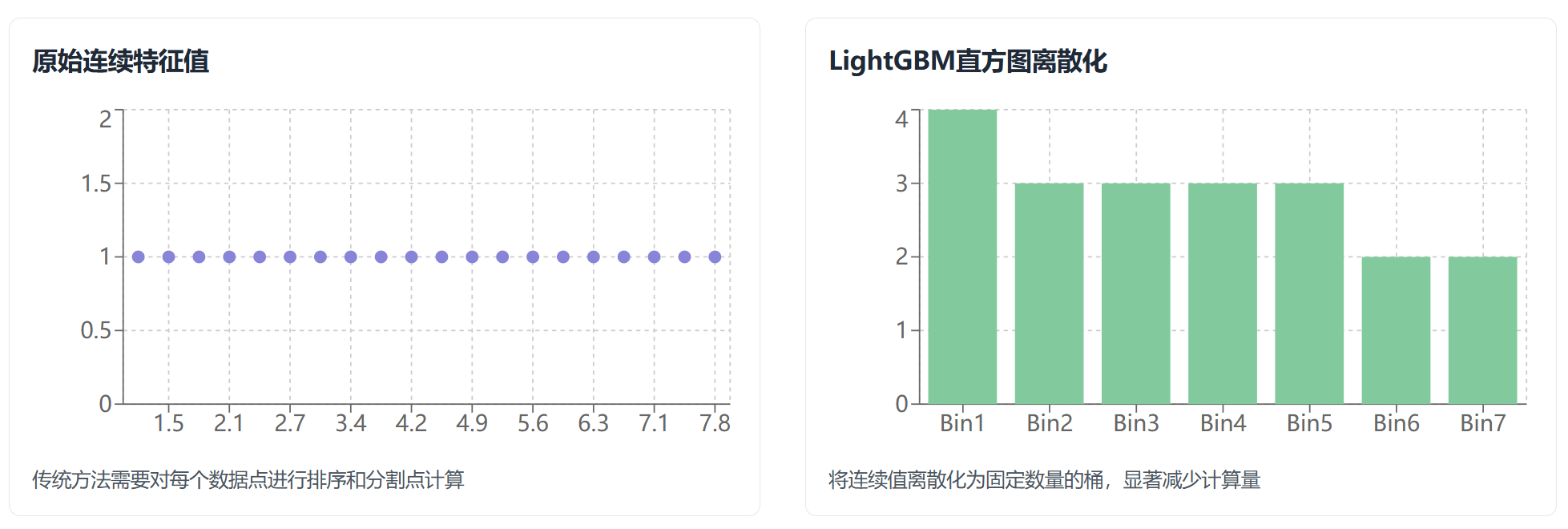
直方图优化

遍历每个特征和其中的值在数据量大的情况下是非常耗时的操作。XGBoost通过提前将数据进行排序以便快速找到最佳分割点，但仍然需要遍历全部数据。LightGBM通过将数据分桶，将时间复杂度从 O(n_{data} \times n_{features}) 降到了 O(n_{bins} \times n_{features}) 。

通常情况下LightGBM会将所有数据分为255个桶，再遍历每个桶找到最佳分割点。这种方式的好处是减少了时间复杂度，但也存在数据粒度不够细，损失了数据之间微小差异的特征，导致最佳分割点被埋藏在某个桶内部，最终导致过拟合的问题。

可视化理解：

计算残差

前面提到，在Boosting策略中，每个学习器需要计算上一个学习器和实际数据的残差。但是实际中GBDT模型采用牛顿近似法得到牛顿步长，再乘以学习率作为残差。

这样做的好处是通过牛顿近似法可以得到最佳的优化方向，而残差只是单独的描述了两个数据的差异，从具体公式理解：

对于任意损失函数L(y, \hat{y})，我们要找到最优的调整量\Delta：

使用二阶泰勒展开：

其中：

对 \Delta求导并令其为0：

得到最优调整：

这里的一阶导数（梯度）描述了方向，二阶导数（海塞矩阵）描述了当前的坡度。

从最后的 \Delta^*的表达式直观理解：

• g > 0 时，损失函数坡度向上，取负向反方向移动

• g < 0 时，损失函数坡度向下，取负向正方向移动

• h 描述了损失函数在当前点的坡度大小，坡度越大，损失函数在当前点越陡峭，整体分数值越小，代表移动一小步就可以下降一大步，反之亦然。