人工智能 - 构建一个井字棋人工智能
人工智能 - 构建一个井字棋人工智能
选取Python语言
量化棋盘
井字棋是一个九宫格,可以使用0-8连续编号来表示
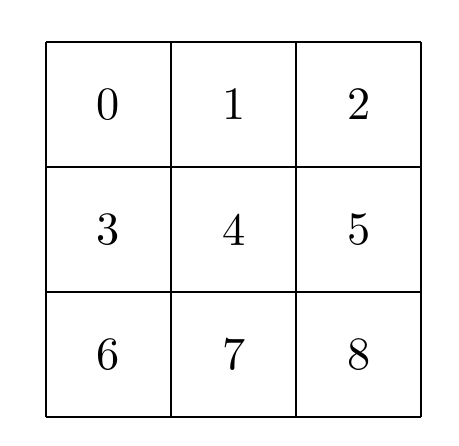
将其扁平化

棋盘对称性与局面判断
注意到九宫格具有对称性,所以我们可以通过对称来减少局面的可能性
同时,我们还需要一些方法来判断局面是否结束
所以创建一个BoardUtils工具类,方面后面使用
对称性例图:Y轴对称
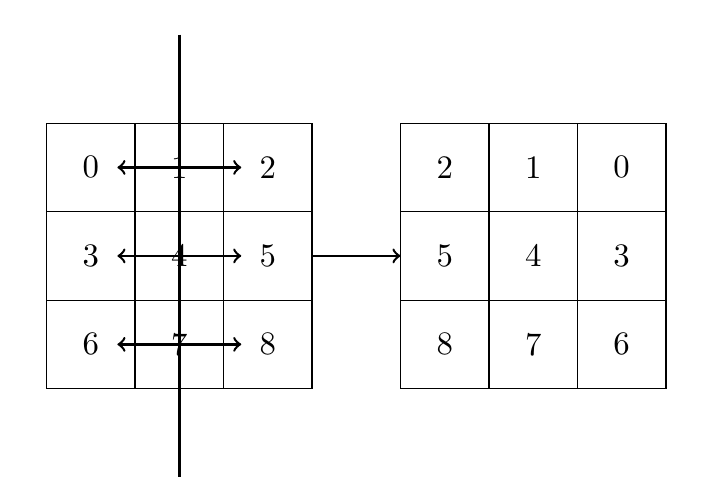
transform_matrix = [
[0,1,2,3,4,5,6,7,8],
[2,1,0,5,4,3,8,7,6],
[6,7,8,3,4,5,0,1,2],
[8,5,2,7,4,1,6,3,0],
[0,3,6,1,4,7,2,5,8],
[6,3,0,7,4,1,8,5,2],
[8,7,6,5,4,3,2,1,0],
[2,5,8,1,4,7,0,3,6]
]
class BoardUtils:
def resort(board, order):
res = []
for i in order:
res.append(board[i])
return res
def flip_and_rotate_board(board):
res=[]
for transform in transform_matrix:
res.append(BoardUtils.resort(board, transform))
return res
调用 BoardUtils.flip_and_rotate_board 方法,可以返回一个棋盘所有8种可能的对称性
以及一些判断方法:
straight_lines = [(0,1,2),(3,4,5),(6,7,8),(0,3,6),(1,4,7),(2,5,8),(0,4,8),(2,4,6)]
def get_3_element_in_board(board: list, index):
return (board[index[0]], board[index[1]], board[index[2]])
def get_winner(board):
for index in straight_lines:
e = BoardUtils.get_3_element_in_board(board, index)
if e.count(0) == 3:
return 0
elif e.count(1) == 3:
return 1
return -1
def is_finish(board):
if BoardUtils.get_winner(board) != -1:
return True
return board.count(-1) == 0BoardUtils.get_winner(b) 判断胜者
BoardUtils.is_finish(b) 判断局面是否结束
构建博弈树
先构建博弈树,将所有可能的情况存在树里
这里我采用一个二维列表,里面一层的每个列表代表树的每一层
同时创建一个Board类,代表棋盘
class Board:
def __init__(self, board):
self.board = board
self.value = -999
self.sub_indexes = []
tree = [
[
Board([-1,-1,-1,-1,-1,-1,-1,-1,-1])
],
[]
]self.board代表棋盘的列表
self.value代表棋盘的价值,这个值我们之后通过minimax计算,所以现在先留空,设置个-999
self.sub_indexes代表这种情况的所有子情况在树中的位置
接下来生成这个树
创建generate方法,接下来代码都是在generate方法里的
def generate(depth):
father_boards = tree[depth-1]depth代表当前生成的深度,则上层所有局面都在tree[depth-1]里
new = False
for father_board in father_boards:
if BoardUtils.is_finish(father_board.board):
continuenew代表一个标志,标志着当前层是否新建了一种局面,如果所有循环结束之后仍然没有新的局面,则说明到了树的最低端
遍历所有父局面,如果父局面已经结束了,那么就跳过
for i in range(len(father_board.board)):
if father_board.board[i] == -1:
b = father_board.board.copy()
# 角色
b[i] = (depth-1)%2再在这一层循环中遍历当前父局面所有的子局面
由于第1层是X下完,第2层是O下完,第三层又是X下完
可以得出当前下棋的人和深度的关系为 (depth-1)%2
接下来判断这一层其他子局面内是否和当前子局面对称后有重复的情况
如果没有重复就加入这一层
is_duplicated = False
for j, transformed in enumerate(BoardUtils.flip_and_rotate_board(b)):
for i, board in enumerate(tree[depth]):
if transformed ==board.board:
is_duplicated = True
loc = (depth, i)
if loc not in father_board.sub_indexes:
father_board.sub_indexes.append((loc,j))
if is_duplicated == True:
break
else:
new = True
loc = (depth, len(tree[depth]))
if loc not in father_board.sub_indexes:
father_board.sub_indexes.append((loc,0))
tree[depth].append(Board(b))加入层之后还要对父局面的 sub_indexes 进行更新,注意这里是以元组 (loc, j) 形式存储的,目的是如果是对称重复的情况,那么就保存对称的形式,然后再加入sub_indexes
j的数字代表着变换在前面定义的 transform_matrix 列表里的索引
如果没有任何重复,那么j就是0,也就代表着 transform_matrix 中的 [0,1,2,3,4,5,6,7,8]这种对称情况,也就是不变
跳出这两个循环后,进行递归操作:
if new:
tree.append([])
generate(depth+1)如果当前层新增了局面,那么就在树中添加一层,并且递归调用generate(depth+1)生成下一层,反之函数结束
最后调用 generate(1) 开始生成
完整代码
def generate(depth):
father_boards = tree[depth-1]
new = False
for father_board in father_boards:
if BoardUtils.is_finish(father_board.board):
continue
for i in range(len(father_board.board)):
if father_board.board[i] == -1:
b = father_board.board.copy()
# 角色
b[i] = (depth-1)%2
is_duplicated = False
for j, transformed in enumerate(BoardUtils.flip_and_rotate_board(b)):
for i, board in enumerate(tree[depth]):
if transformed ==board.board:
is_duplicated = True
loc = (depth, i)
if loc not in father_board.sub_indexes:
father_board.sub_indexes.append((loc,j))
if is_duplicated == True:
break
else:
new = True
loc = (depth, len(tree[depth]))
if loc not in father_board.sub_indexes:
father_board.sub_indexes.append((loc,0))
tree[depth].append(Board(b))
generate(1)Minimax评估
树生成完之后,我们需要对每个局面进行评估,这样才能采取出最优策略
但是需要注意的是,Minimax评估值取决于AI先手还是后手,所以不能马上对局面进行评估
Minimax的算法内容:
如果是叶子节点(局面已结束),那么将我方获胜的价值标为999(模拟正无穷),敌方获胜的价值标为-999(模拟负无穷)
如果不是叶子节点,则价值为我方所有可能获胜的情况数-敌方所有可能获胜的情况数
是自己下的局面为Max局面,是他人下的局面为Min局面
Max局面的评估值是所有子节点中最小的值,Min局面的评估值是所有子局面中最小的值
对一个局面的minimax进行计算,我们可以指定minimax递归N层,不需要到底
对于第二条计算的详细过程:
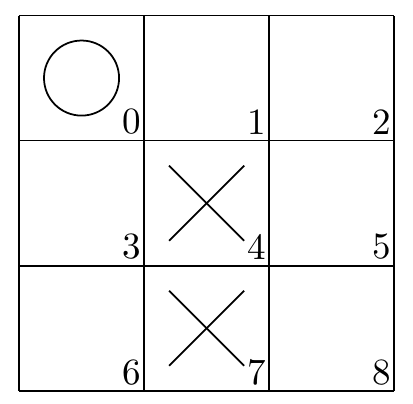
例如以上情况:
对于棋子X,有(147)(258)(345)(678)(246) 五种获胜情况
对于棋子O,有(012)(036)(258) 三种获胜情况
所以棋子X的评估值为5-3=2,棋子O的评估值为3-5=-2
两者相加为0,属于零和博弈
原因也很简单,因为Min局面是对方下,我们就默认敌方会下对我们最差的那一手
而Max局面是我们下,我们就要选择对自己最有利的那一手
接下来进入代码部分
在写评估函数前,需要新增一些工具方法,方便我们调用
def tree_index_2d(index):
global tree
return tree[index[0]][index[1]]
def tree_index_2d_modify(index, val):
global tree
tree[index[0]][index[1]] = val这两个方法分别可以便捷的通过二维坐标获取或修改树中的值
接下来进入Minimax函数:
def minimax(index, role, n):n代表当前递归的层数,
index代表当前需要计算minimax值的局面在tree中的位置,
role代表是X还是O
now+=1
board = tree_index_2d(index)
sub_values = []
if len(board.sub_indexes) == 0:
return calc_value(board.board, role)先将层数+1,然后判断当前局面是否已经结束,如果已经结束就直接输出这个局面的价值
for sub_index,_ in board.sub_indexes:
sub_board = tree_index_2d(sub_index)
if now == 4:
sub_values.append(calc_value(sub_board.board, role))
else:
sub_values.append(minimax2(sub_index, role, now))
value = 0
if (index[0]+role)%2==0:
value = max(sub_values)
else:
value = min(sub_values)
return value如果没有结束,那么进入子局面的评估
如果递归的层数到达了4(这个4可以是其他值,代表最大递归层数,也就是minimax的深度),则将子局面的评估值作为子局面的minimax值
如果没达到,就计算子局面的minimax值
最后判断当前是min层还是max层,并输出结果
完整代码
def minimax(index, role, now):
now+=1
board = tree_index_2d(index)
sub_values = []
if len(board.sub_indexes) == 0:
return calc_value(board.board, role)
for sub_index,_ in board.sub_indexes:
sub_board = tree_index_2d(sub_index)
if now == 4:
sub_values.append(calc_value(sub_board.board, role))
else:
sub_values.append(minimax2(sub_index, role, now))
value = 0
if (index[0]+role)%2==0:
value = max(sub_values)
else:
value = min(sub_values)
return value
决策
有了minimax和博弈树,我们就可以进行决策了
先加上我们所需的工具函数:
def reverse_transform(board, method):
if method<=4 or method==6:
return BoardUtils.resort(board, transform_matrix[method])
else:
return BoardUtils.resort(board, reversed(transform_matrix[method]))这个函数可以根据对称的方法,把对称后的局面变成对称前的局面
对于所有轴对称和180度对称,采取原封不动的对称方式返回
对于其他情况(90度旋转对称,270度旋转对称),采取反转后的对称方式返回
定义一个AI类:
class AI:
# 输入深度和棋盘
# 输出变换方式, 树中的位置
def get_board_loc_in_tree(depth, board):
for method, transformed in enumerate(BoardUtils.flip_and_rotate_board(board)):
for i, board_in_tree in enumerate(tree[depth]):
if transformed == board_in_tree.board:
return (method, (depth, i))
因为玩家输入的棋盘不一定在我们的树中(对称性),所以这个方法用于查询玩家的棋盘对应树中的棋盘位置,并输出对称方式
接下来是决策函数:
def make_choice(depth, board, role):
method, board_loc = AI.get_board_loc_in_tree(depth, board)
board_in_tree = tree_index_2d(board_loc)
best = None
for sub_index,m in board_in_tree.sub_indexes:
cond = False
val = minimax(sub_index, role, 0)
if (depth+role)%2==0:
cond = best!=None and val > best[0]
else:
cond = best!=None and val < best[0]
if best==None or cond:
best = (val, sub_index, m)
if best!=None:
new_board = tree_index_2d(best[1])
else:
new_board = board_in_tree
return BoardUtils.reverse_transform(BoardUtils.reverse_transform(new_board.board, best[2]), method)这一段代码基本就是进行一次minimax,找出最好的选择
值得一提的是最后的reverse_transform,进行了两次
因为这里面涉及到两次对称:第一次是玩家棋盘到树中局面的对称,第二次是树中局面到树中局面的子局面的对称
完整代码
class AI:
# 输入深度和棋盘
# 输出变换方式, 树中的位置
def get_board_loc_in_tree(depth, board):
for method, transformed in enumerate(BoardUtils.flip_and_rotate_board(board)):
for i, board_in_tree in enumerate(tree[depth]):
if transformed == board_in_tree.board:
return (method, (depth, i))
def make_choice(depth, board, role):
method, board_loc = AI.get_board_loc_in_tree(depth, board)
board_in_tree = tree_index_2d(board_loc)
best = None
for sub_index,m in board_in_tree.sub_indexes:
cond = False
val = minimax(sub_index, role, 0)
if (depth+role)%2==0:
cond = best!=None and val > best[0]
else:
cond = best!=None and val < best[0]
if best==None or cond:
best = (val, sub_index, m)
if best!=None:
new_board = tree_index_2d(best[1])
else:
new_board = board_in_tree
return BoardUtils.reverse_transform(BoardUtils.reverse_transform(new_board.board, best[2]), method)玩家交互
这一块不涉及到什么,直接上代码
def show_board(board):
symbol = {-1:"_", 0:"X", 1:"O"}
b = board.copy()
for i in range(len(b)):
b[i] = symbol[b[i]]
print("====================")
print(f' {b[0]} {b[1]} {b[2]}')
print(f' {b[3]} {b[4]} {b[5]}')
print(f' {b[6]} {b[7]} {b[8]}')
print(f'===================')
def game():
now_turn = 0
player_role = int(input("请选择你的棋子( 0=X先手 1=O后手 ): "))
ai_role = 1-player_role
depth = 0
board = [-1,-1,-1,-1,-1,-1,-1,-1,-1]
game_over = False
while not game_over:
if now_turn == player_role:
show_board(board)
chess_loc = int(input("输入你要下的地方(0-8): "))
board[chess_loc] = player_role
depth+=1
else:
print("正在计算...")
board = AI.make_choice(depth, board, ai_role)
depth+=1
now_turn= 1-now_turn
winner = BoardUtils.get_winner(board)
if winner != -1:
show_board(board)
print("恭喜"+{player_role:"玩家",ai_role:"AI"}[winner]+"获胜!")
game_over = True
elif BoardUtils.is_finish(board):
show_board(board)
print("平局!")
game_over = True
game()完整代码
straight_lines = [(0,1,2),(3,4,5),(6,7,8),(0,3,6),(1,4,7),(2,5,8),(0,4,8),(2,4,6)]
transform_matrix = [
[0,1,2,3,4,5,6,7,8],
[2,1,0,5,4,3,8,7,6],
[6,7,8,3,4,5,0,1,2],
[8,5,2,7,4,1,6,3,0],
[0,3,6,1,4,7,2,5,8],
[6,3,0,7,4,1,8,5,2],
[8,7,6,5,4,3,2,1,0],
[2,5,8,1,4,7,0,3,6]
]
class BoardUtils:
def get_3_element_in_board(board: list, index):
return (board[index[0]], board[index[1]], board[index[2]])
def get_winner(board):
for index in straight_lines:
e = BoardUtils.get_3_element_in_board(board, index)
if e.count(0) == 3:
return 0
elif e.count(1) == 3:
return 1
return -1
def is_finish(board):
if BoardUtils.get_winner(board) != -1:
return True
return board.count(-1) == 0
def resort(board, order):
res = []
for i in order:
res.append(board[i])
return res
def flip_and_rotate_board(board):
res=[]
for transform in transform_matrix:
res.append(BoardUtils.resort(board, transform))
return res
def reverse_transform(board, method):
if method<=4 or method==6:
return BoardUtils.resort(board, transform_matrix[method])
else:
return BoardUtils.resort(board, reversed(transform_matrix[method]))
class Board:
def __init__(self, board):
self.board = board
self.value = -999
self.sub_indexes = []
def __str__(self):
return self.board.__str__()
def __repr__(self):
return self.__str__()
tree = [
[
Board([-1,-1,-1,-1,-1,-1,-1,-1,-1])
],
[]
]
def tree_index_2d(index):
global tree
return tree[index[0]][index[1]]
def generate(depth):
father_boards = tree[depth-1]
new = False
for father_board in father_boards:
if BoardUtils.is_finish(father_board.board):
continue
for i in range(len(father_board.board)):
if father_board.board[i] == -1:
b = father_board.board.copy()
# 角色
b[i] = (depth-1)%2
is_duplicated = False
for j, transformed in enumerate(BoardUtils.flip_and_rotate_board(b)):
for i, board in enumerate(tree[depth]):
if transformed ==board.board:
is_duplicated = True
loc = (depth, i)
if loc not in father_board.sub_indexes:
father_board.sub_indexes.append((loc,j))
if is_duplicated == True:
break
else:
new = True
loc = (depth, len(tree[depth]))
if loc not in father_board.sub_indexes:
father_board.sub_indexes.append((loc,0))
tree[depth].append(Board(b))
if new:
tree.append([])
generate(depth+1)
def calc_value(board, role):
my_chance = 0
enemy_chance = 0
for combination in straight_lines:
chesses = BoardUtils.get_3_element_in_board(board, combination)
if chesses.count(1-role) == 0:
my_chance+=1
elif chesses.count(role) == 0:
enemy_chance+=1
if chesses.count(1-role) == 3:
return -9999
if chesses.count(role) == 3:
return 9999
return my_chance-enemy_chance
def minimax(index, role, now):
now+=1
board = tree_index_2d(index)
sub_values = []
if len(board.sub_indexes) == 0:
return calc_value(board.board, role)
for sub_index,_ in board.sub_indexes:
sub_board = tree_index_2d(sub_index)
if now == 4:
sub_values.append(calc_value(sub_board.board, role))
else:
sub_values.append(minimax(sub_index, role, now))
value = 0
if (index[0]+role)%2==0:
value = max(sub_values)
else:
value = min(sub_values)
return value
generate(1)
class AI:
# 输入深度和棋盘
# 输出变换方式, 树中的位置
def get_board_loc_in_tree(depth, board):
for method, transformed in enumerate(BoardUtils.flip_and_rotate_board(board)):
for i, board_in_tree in enumerate(tree[depth]):
if transformed == board_in_tree.board:
return (method, (depth, i))
def make_choice(depth, board, role):
method, board_loc = AI.get_board_loc_in_tree(depth, board)
board_in_tree = tree_index_2d(board_loc)
best = None
for sub_index,m in board_in_tree.sub_indexes:
cond = False
val = minimax(sub_index, role, 0)
if (depth+role)%2==0:
cond = best!=None and val > best[0]
else:
cond = best!=None and val < best[0]
if best==None or cond:
best = (val, sub_index, m)
if best!=None:
new_board = tree_index_2d(best[1])
else:
new_board = board_in_tree
return BoardUtils.reverse_transform(BoardUtils.reverse_transform(new_board.board, best[2]), method)
def show_board(board):
symbol = {-1:"_", 0:"X", 1:"O"}
b = board.copy()
for i in range(len(b)):
b[i] = symbol[b[i]]
print("====================")
print(f' {b[0]} {b[1]} {b[2]}')
print(f' {b[3]} {b[4]} {b[5]}')
print(f' {b[6]} {b[7]} {b[8]}')
print(f'===================')
def game():
now_turn = 0
player_role = int(input("请选择你的棋子( 0=X先手 1=O后手 ): "))
ai_role = 1-player_role
depth = 0
board = [-1,-1,-1,-1,-1,-1,-1,-1,-1]
game_over = False
while not game_over:
if now_turn == player_role:
show_board(board)
chess_loc = int(input("输入你要下的地方(0-8): "))
board[chess_loc] = player_role
depth+=1
else:
print("正在计算...")
board = AI.make_choice(depth, board, ai_role)
depth+=1
now_turn= 1-now_turn
winner = BoardUtils.get_winner(board)
if winner != -1:
show_board(board)
print("恭喜"+{player_role:"玩家",ai_role:"AI"}[winner]+"获胜!")
game_over = True
elif BoardUtils.is_finish(board):
show_board(board)
print("平局!")
game_over = True
game()
Comments