什么?在想LSTM的事?
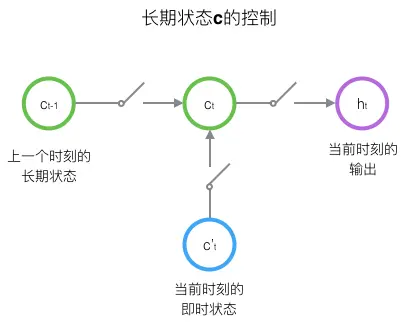
在t时刻,LSTM有三个输入(都是向量):
x_t(当前时刻的输入)
h_{t-1}(上一时刻的输出)
c_{t-1}(上一时刻的单元状态,LSTM重要的部分)
两个输出:
h_t(当前时刻的输出)
c_t(当前时刻的单元状态)
门
门实质上是一层全连接层,输入为一个向量,输出范围为 (0,1)的实数向量。
大概的表示: g(x) = \sigma(Wx+b)
门的作用大概是控制能通过多少输入向量,实现方法是将门输出的向量与原输入向量做点积,如果门输出向量靠近0,那么原输入向量通过的就少,靠近一通过的就多,所以叫门
在接下来对三个门的介绍中可以发现,LSTM中的门都是由 h_{t-1}和 x_t拼接成的向量进行线性变换得到的
遗忘门控制要保留多少 c_{t-1}到 c_t
输入门控制要保留多少 x_t到 c_t
输出门控制要保留多少 c_t到 h_t
遗忘门
遗忘门控制要保留多少 c_{t-1}到 c_t
数学表达: f_t = \sigma(W_f\cdot Concat[h_{t-1}, x_t] + b_f) ,注意这里的 f_t就是遗忘门,是一个向量,并且经过sigmoid激活后范围限制到 (0,1)
设输入的维度为 d_x,隐藏层的维度为 d_h,单元状态维度为 d_c(通常 d_c = d_h,下面都写作 d_h),则 W_f的维度为 d_h \times (d_h + d_x) (因为遗忘门控制的是 c_{t-1},所以维度和单元状态的维度保持一致)
但事实上是 W_f由两个矩阵组成,分别全连接再拼接:
\begin{bmatrix} W_f \end{bmatrix} \begin{bmatrix} h_{t-1} \\ x_t \end{bmatrix} = \begin{bmatrix} W_{fh} & W_{fx} \end{bmatrix} \begin{bmatrix} h_{t-1} \\ x_t \end{bmatrix} = W_{fh} h_{t-1} + W_{fx}x_{t}
维度表示:
W_{fh} = Matmul((d_h \times d_h), (d_h \times 1)) = (d_h \times 1) \\ W_{fx} = Matmul((d_h \times d_x), (d_x \times 1)) = (d_h \times 1)
输入门
输入门控制要保留多少 x_t到 c_t
输入门的计算:
i_t = \sigma(W_i\cdot Concat[h_{t-1},x_t]+b_i) ,这里的 i_t就是输入门
i_t的维度: d_h \times 1 (向量)
接下来,再计算出当前输入的单元状态 \widetilde{c}_t:
\widetilde{c}_t = tanh(W_c\cdot Concat[h_{t-1}, x_t] + b_c)
\widetilde{c}_t的维度: d_h \times 1 (向量)
这是纯由当前输入和上一层输出计算出来的
接下来计算当前单元状态 c_t:
c_t = f_t \circ c_{t-1} + i_t \circ \widetilde{c}_t
c_t的维度: d_h \times 1 (向量)
这里体现了将门向量与原向量点积
至此当前单元状态 c_t计算完毕。
输出门
输出门控制要保留多少 c_t到 h_t
o_t = \sigma(W_o \cdot Concat[h_{t-1}, x_t] + b_o)
o_t的维度: d_h \times 1 (向量)
计算最终输出 h_t:
h_t = o_t \circ tanh(c_t)
我也不知道这部分起什么副标题
c_t = f_t \circ c_{t-1} + i_t \circ \widetilde{c}_t
从此式可以看出:单元状态的本质是上一个单元状态经过遗忘门后再加上输入的单元状态,所以整体的变化不会太大,也符合单元状态的长期特征,
而相比之下, h_t的变化就大得多
联系实际(Pytorch)
关于实际应用中pytorch的几个参数:
input_size,即输入数据的特征维数,上文的 d_xhidden_size,即隐藏层的维数,上文的 d_h,注意这里只是指LSTM输出的维数,而不是最终的,实践中后面可以加一层全连接之类的num_layers,即循环神经网络层数(竖直方向堆叠),
前一层的隐藏输出向量,对应下一层的输入向量
偷了张图可能会更直观些: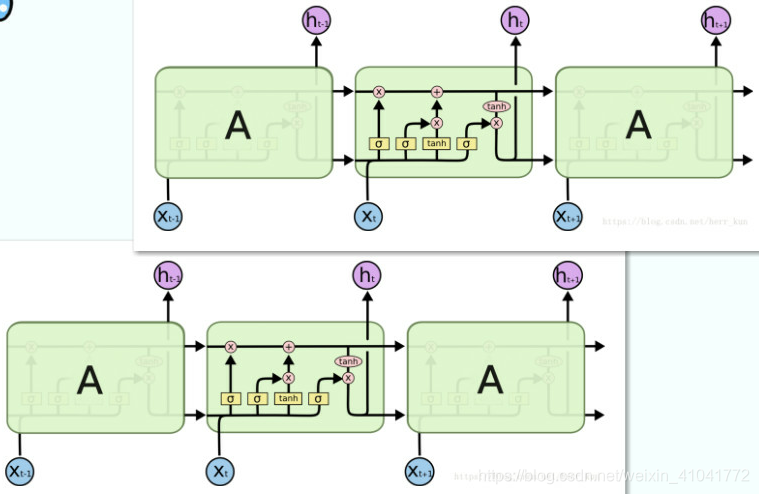
Comments